ゴールキックを遠くに飛ばすのに最適な打ち出し角度は？

2023.05.25　written by Gaku Morita (SPLYZA Inc.)

ハンマー投げ、砲丸投げなど、槍投げなど物体を遠くに飛ばす競技はたくさんあります。バスケ、野球、ハンドボールなどの球技でもボールを遠くに飛ばしたいシーンがありますよね。サッカーでもボールを遠くに飛ばしたいシーンはあります。ゴールキックでは特にボールを遠くまで飛ばしたいと思うことが多くあるのではないでしょうか。

この記事では、サッカーの試合でのゴールキック時に「どんな打ち出し角度でボールを蹴り上げれば"最も遠く"までボールを飛ばす事ができるか？」を考えて行きます。

ゴールキックでボールを蹴って飛ばす時に、蹴る力は大きく影響します。強い力で蹴ると遠くに飛びますし、弱い力で蹴ると当然のごとくあまり飛びません。ただ、今回は打ち出し角度について考えるため、蹴る力は一定として考えて行きます(力積は一定)。

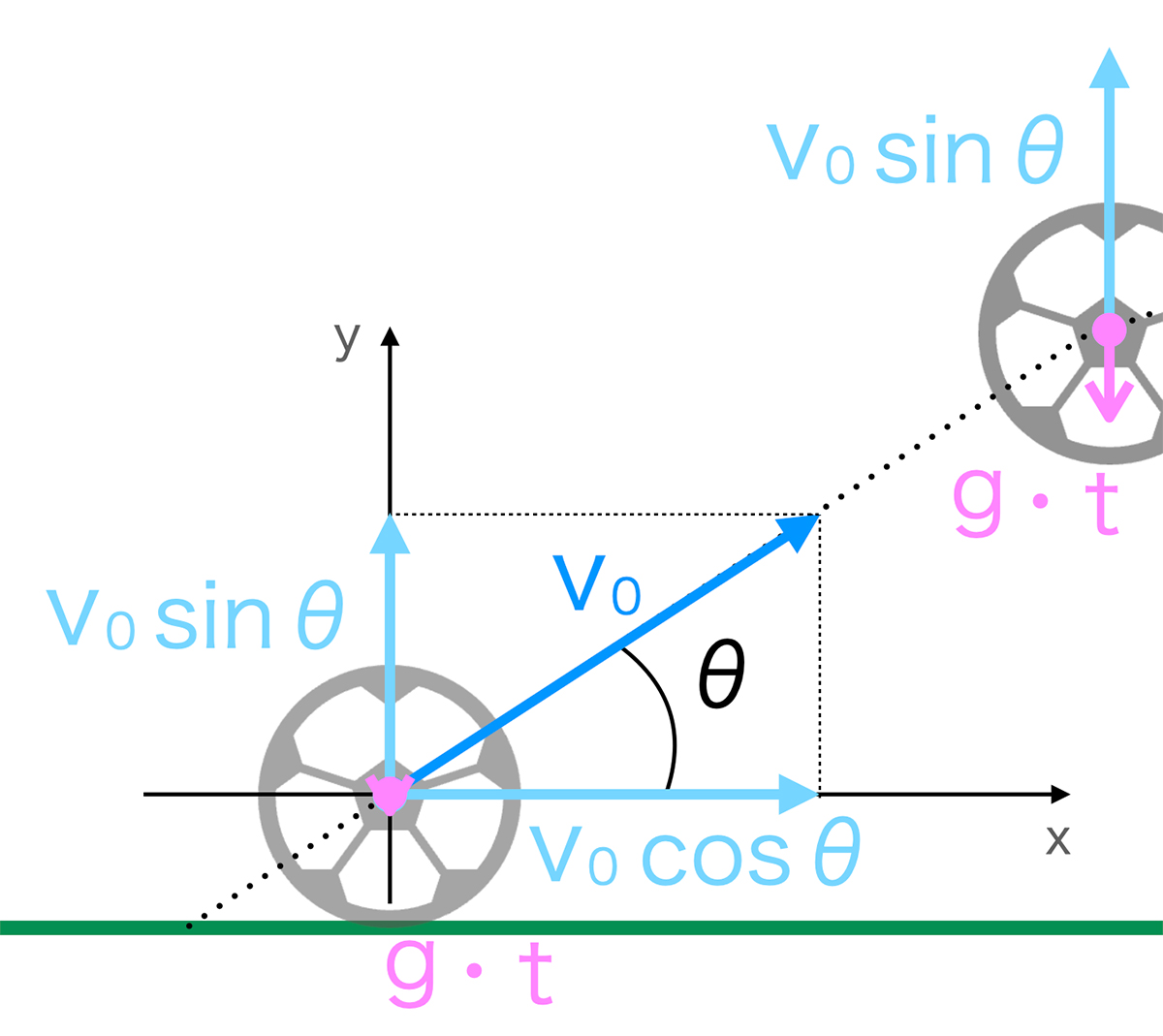
蹴る力が一定だと、打ち出し速度 v₀ [m/s] は一定として考えることができます。以下のような図の中で、ボールが最も遠くに着地する最適な打ち出し角度 θ [deg]を考えて行きましょう。

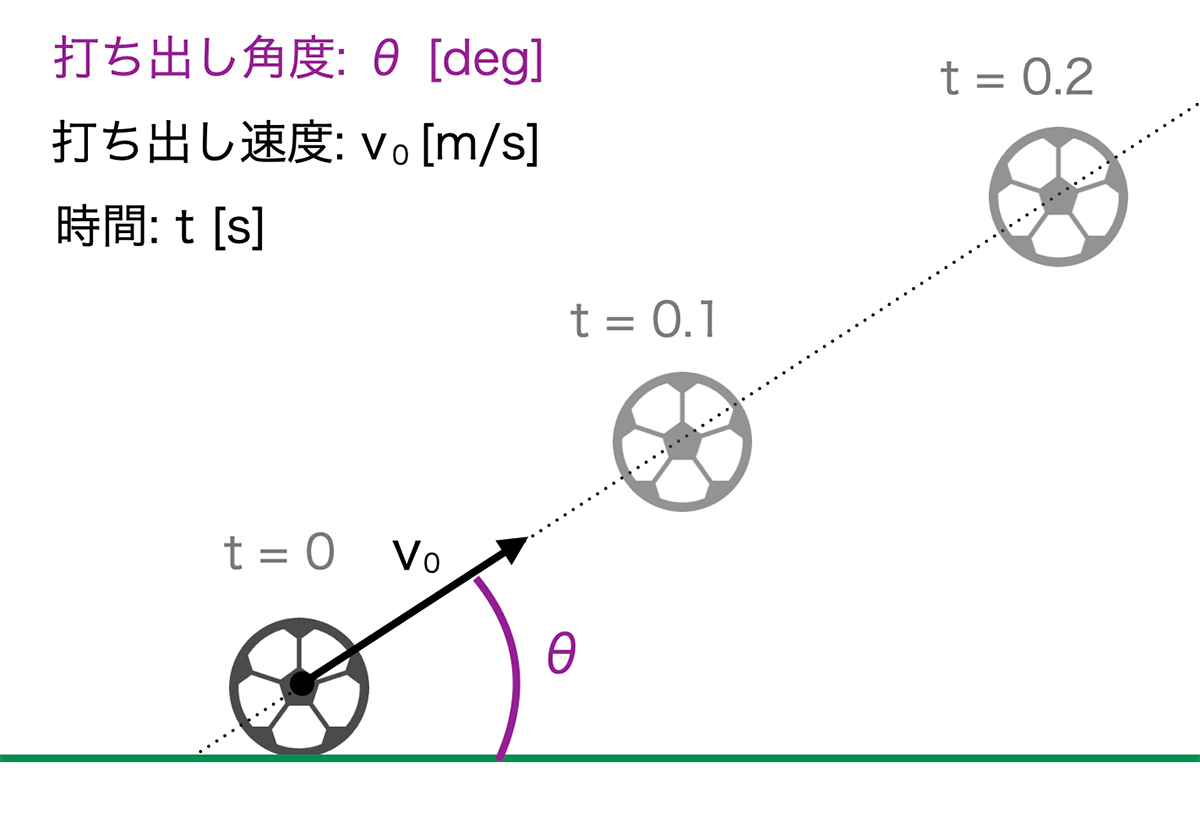
重力を考慮

ボールが打ち出された後、空中にボールがある時にどんな力が作用しているでしょうか。大きく作用する力は重力です。ボールは重力によって、地面に向かって重力加速度 g [m/s²]が常にかかります。

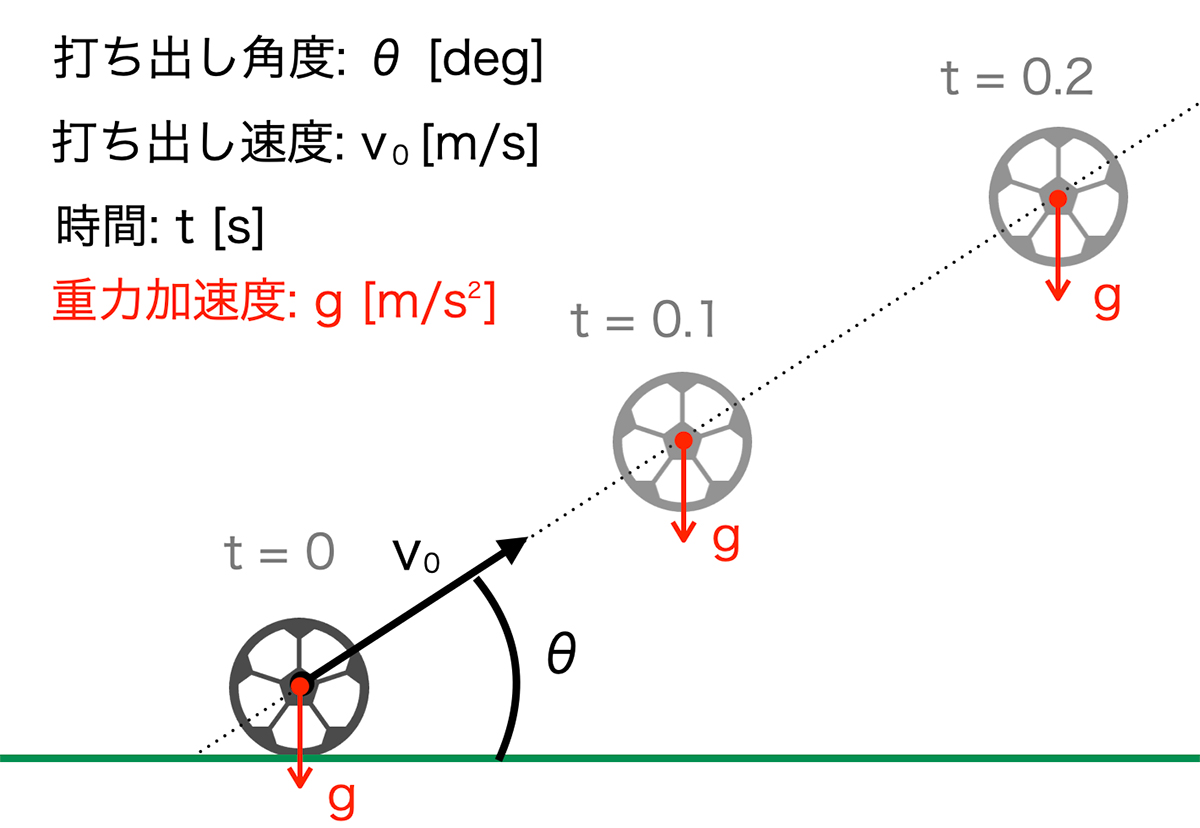
水平方向をx軸、高さ方向をy軸として、y軸方向の重力加速度の影響を考慮します。まずは、ボールの打ち出し速度 v₀ [m/s] をx軸方向、y軸方向に分けます。(速度の分解)

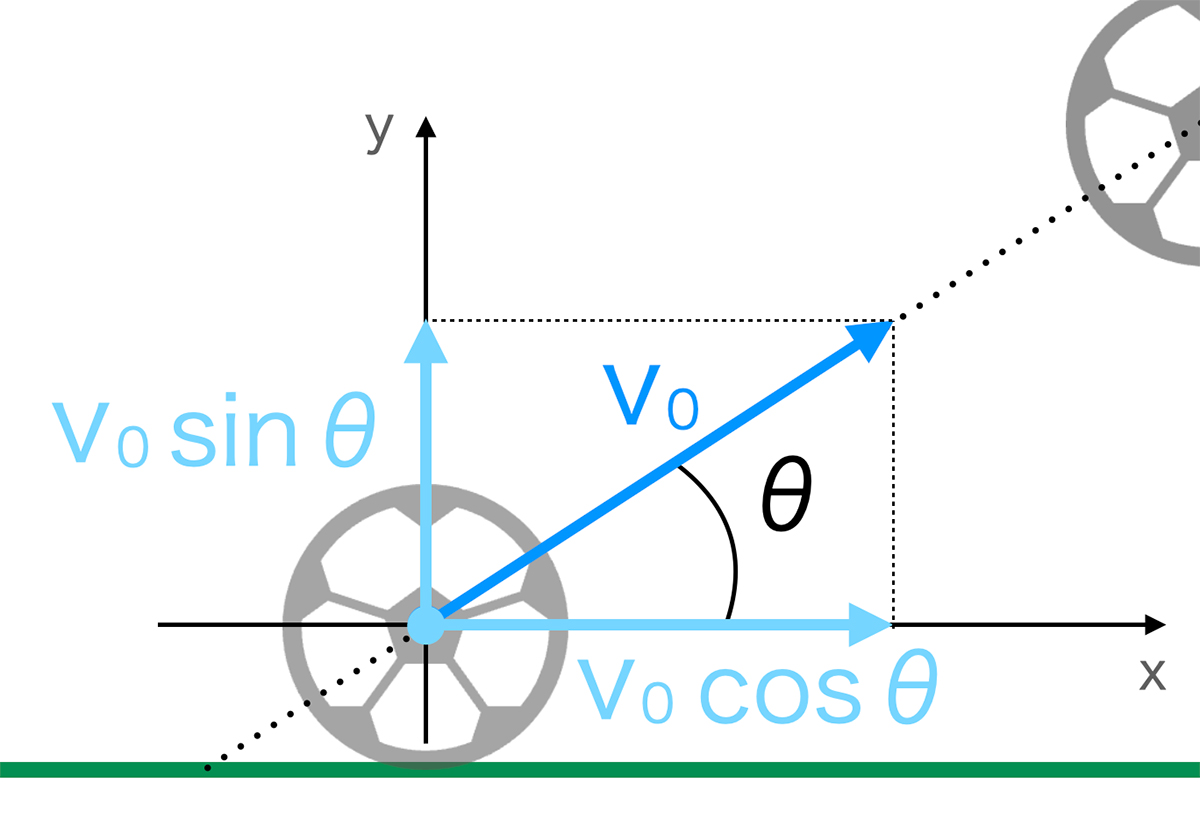
x軸方向、y軸方向の打ち出し速度v_0x [m/s]、v_0y [m/s] はそれぞれ

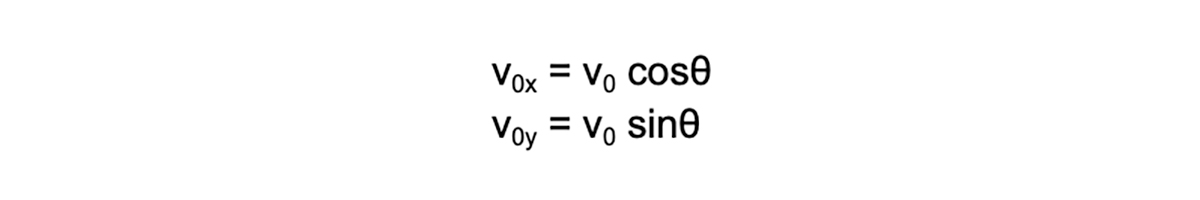
y軸方向の速度は重力加速度 g [m/s²]の影響を受けて、時間 t [s]に応じて変化します。(x軸方向の速度は時間に応じて変化しない)

したがって速度 v_x [m/s]、v_y [m/s]は以下の式で表す事ができます。

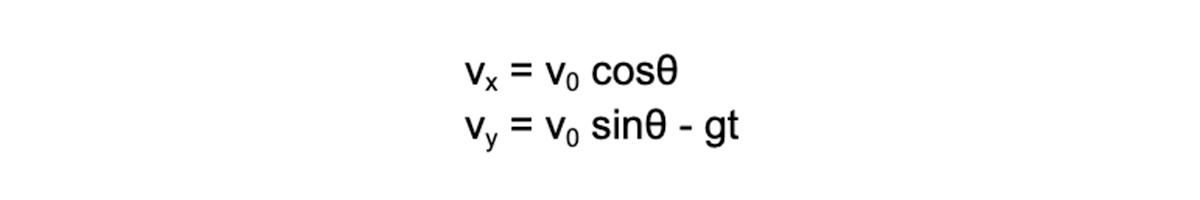
次にこの速度についての式を変位についての式に変換します(時間 t で積分)。時間 t [s]に応じた変位 X [m]、Y [m]はそれぞれ、

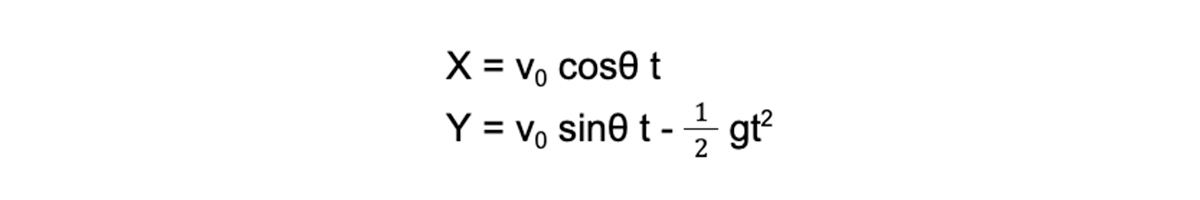
ボールが着地するというのは、Y = 0の時なので、時間 t について解くと、

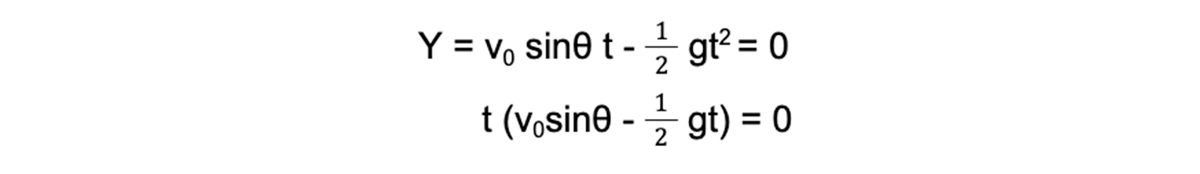
ここで、着地する時の変位 X [m]について考えます。変位 X [m]の式に着地する時の時間 t を代入すると、

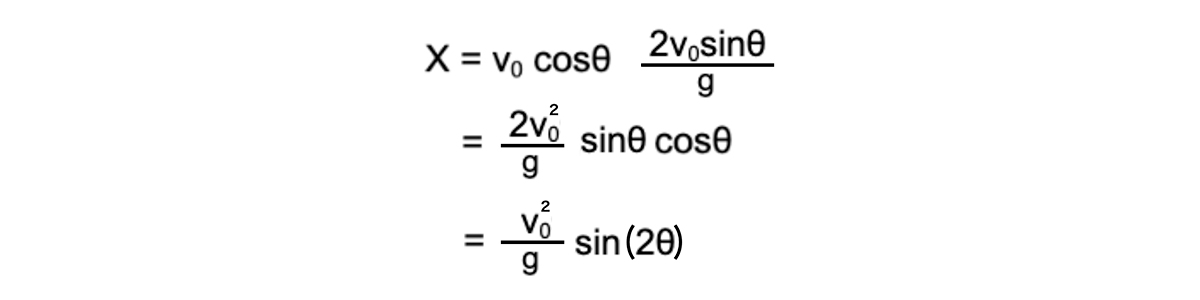
この時、0＜θ＜90 [deg] で sin(2θ) が最大になるのは 2θ = 90 [deg] → θ = 45 [deg] となり、打ち出し角度45 [deg] の時、Xが最大値をとります。つまり重力のみを考慮した時に最も遠くまでボールを飛ばす打ち出し角度は45 [deg]となります。

風を考慮

実際は重力以外にもボールに力はかかります。次に風を考慮してみます。

※ここでは風の力によって一定の加速度が常にかかると仮定して計算しています。

加速度 a [m/s²]がx軸方向にかかるとすると、速度 v_x [m/s]、v_y [m/s]はそれぞれ

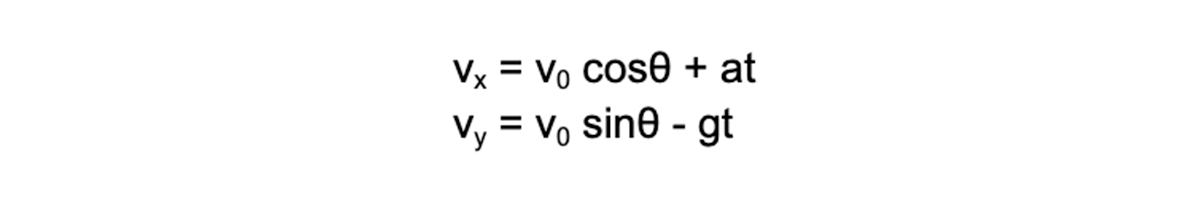
上式に基づいて、打ち出し速度 25 [m/s]、a = 2 [m/s²](追い風)、a = -2 [m/s²](向かい風)の時の最適な角度をシミュレータで計算してみました。

計算シートはこちら

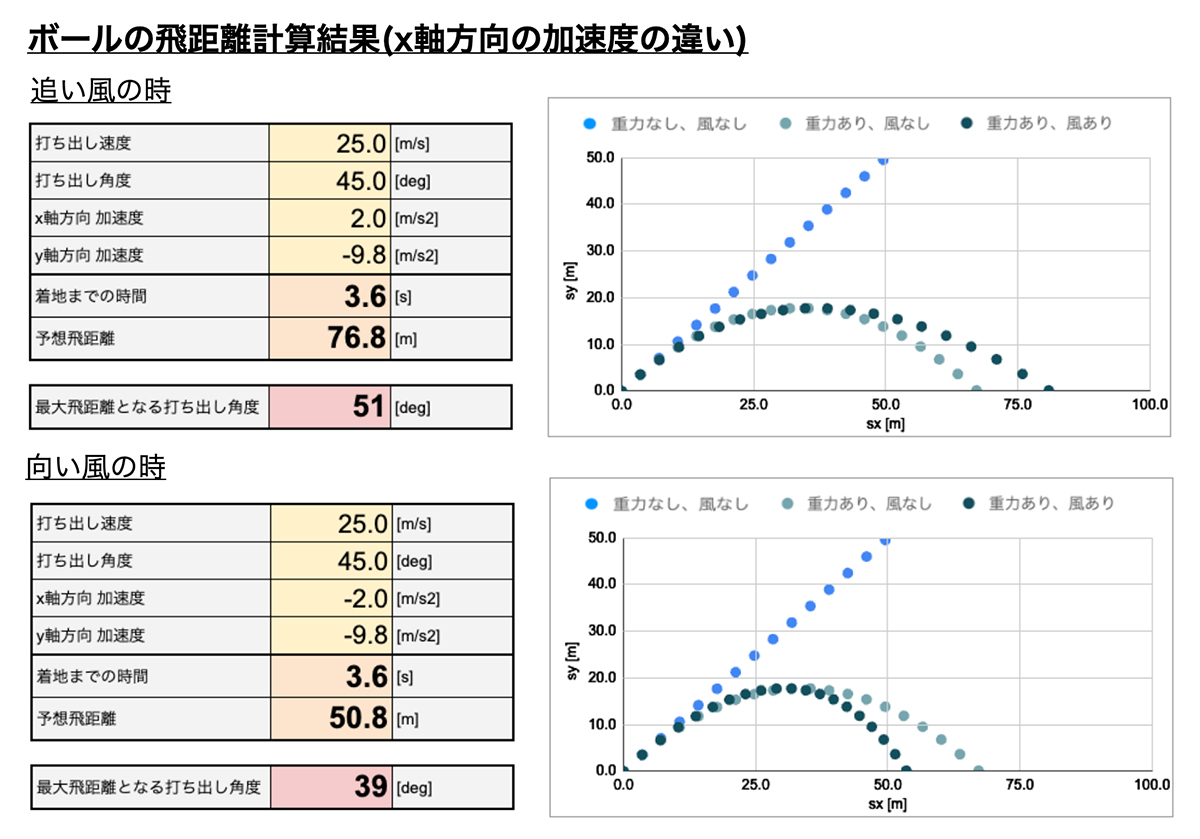
それぞれ最大飛距離となる打ち出し角度は、追い風だと45 [deg]よりも角度は高く、向かい風だと45 [deg]よりも低くなりました。低い打ち出し角度の方が空中にボールがある時間が短くなり、風の影響を受けにくくなります。

まとめ

重力のみを考慮した時、ゴールキックを蹴って遠くに飛ばす時の最適な打ち出し角度は45度です。風の影響を考えると最大飛距離となる打ち出し角度は変わります。低い打ち出し角の方が風の影響を受けづらい為、狙ったところにボールを飛ばしやすいと言えます。

補足

前述した、重力、風以外にも、ボールが大気中の空気に衝突することで生まれる空気抵抗、ボールの回転によって生じる揚力もボールの飛距離には影響します。今回はこれらを考慮せずに計算してみました。

ここでは打ち出し角度45度が遠くボールを飛ばすには最適という結論が得られました。ただ、実際に置いてあるボールを蹴って45度で打ち出すことは可能なのでしょうか？今後、公開を予定している記事では「足の構造から可能かどうか」を考えてみます。