[サッカー×数学] 最強のペナルティーキック理論 - PKでのキック成功率を最大化する角度と速度《夏休みの自由研究》

2024.07.24　written by Daichi Kawano (SPLYZA Inc.)

はじめに

サッカーの試合において、エキサイティングで緊張感あふれる瞬間の一つに「PK(ペナルティーキック)」があります。ゴールまで約11メートルという絶妙の距離で、キッカーとゴールキーパーの心理戦が繰り広げられ、場合によってはその1つのボールの行方が試合の結果を左右することも。チームにおける重大な任務を託されたキッカーは、ゴールキーパーの心理を読み、駆け引きを行いながらシュートを放ちます。しかし、たとえ理想的なキックが出来たとしても、相手GKの好セーブによって弾き返されたり、はたまたゴールポストに直撃、時には枠外に外れてしまう事もままある訳です。

なお、PKにおいてはキッカーが圧倒的に有利(過去のワールドカップにおける統計では、PKの成功率は約8割程度)とされていますが、それでもPKストップを得手としているゴールキーパーは世界中に存在しており、未だに「ペナルティーキックにおける(キッカー側の)完璧な攻略法」は確立されていません。そこで本記事では、数学の力を用いてPK成功率を最大化するための最適な"角度"と"速度"を導き出し、ワールドクラスのGKをも絶望させる(であろう)究極のPK理論を、ガチ半分&ネタ半分で楽しく証明していければと思います。

◾︎ 今も昔も「迷わずフルパワーで叩き込む！」はペナルティーキックのセオリーだ！

独特なステップを刻むジョルジーニョ(現アーセナル)や、コロコロPKでお馴染み遠藤保仁(元ガンバ大阪…etc)など、歴代のペナルティーキックの名手には、各々が独特なテクニックを持ち合わせている場合が多いといえます。ただ今回は(上の動画にもあるように)あくまで、「キーパーが処理できない場所に全力で蹴り込めば案外イケるのでは？」みたいなノリで進めていきますので、再現性の低い”選手固有ムーブ”的なものは対象外とします。

また前提として、この仮説を証明するために「公式で規定されているサイズのフィールドで試技されること」を想定し、そのうえで「ボールとゴールの測定値は国際サッカー連盟(FIFA)のガイドラインに従うこと」とします。加えて、現実ではありえないシュートの威力を設定しても意味がないので、キッカーの能力に関しては「過去、サッカーの試合において公式に記録された数値」を参考にします。(※ボールが受ける風や空気抵抗による影響、またそれに伴うボールの回転数などは無視するものとします。)

前置きが長くなりましたが、早速、具体的な数値を求めていきましょう。

その①: 角度

言うまでもなく、人間の可動域には限界があります。ペナルティーキックにおいても、ゴールキーパーが実際にカバーできる範囲は限られますので、その範囲を「ダイビング・エンベロープ(ゴールキーパーが飛び込める限界の範囲)」と定義します。

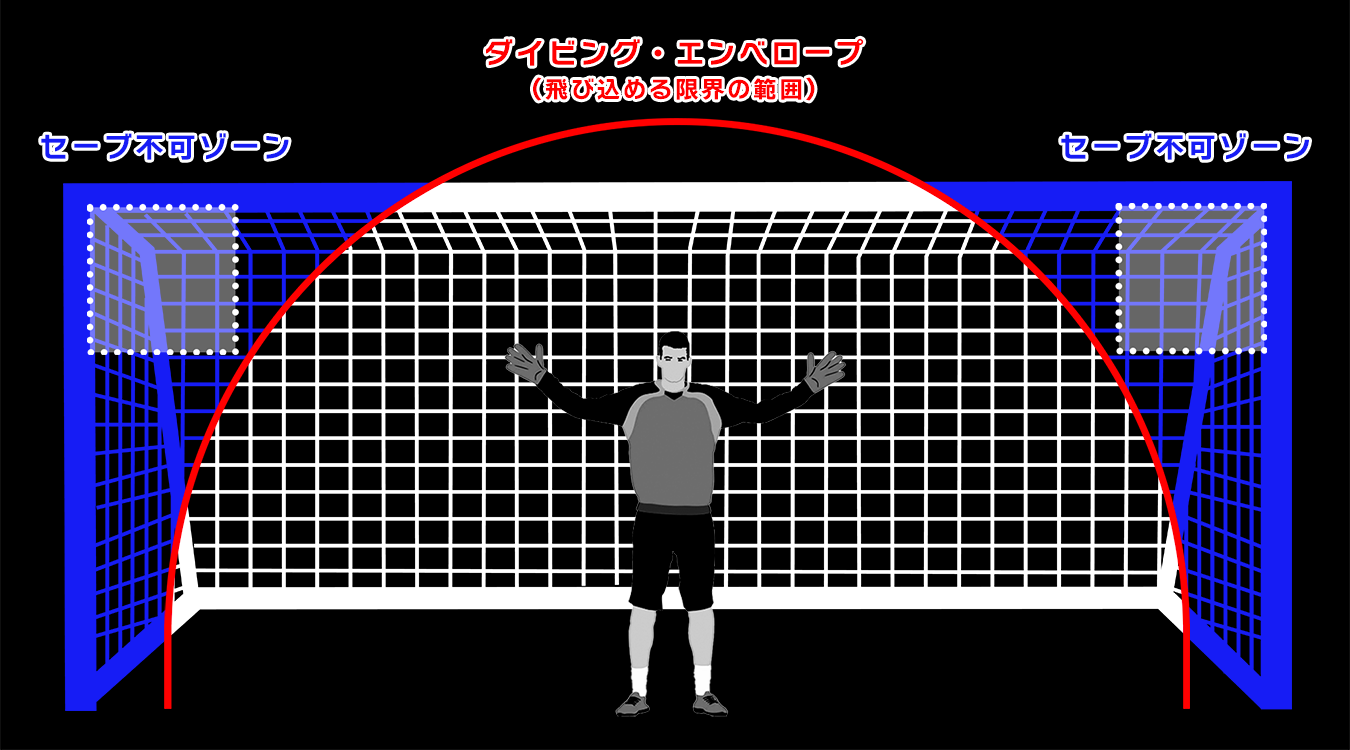図1: 「ダイビング・エンベロープ」＝平均的なゴールキーパーのリーチ(飛び込める限界の範囲)を示している。

サッカーにおいてGKの身長はポジション別で最も高い部類に入る訳ですが、平均189cmとされる体躯において、おおよそ90cmにもなる腕の長さを加味しても、7.3mもあるゴールの幅を全てカバーすることはできません。また、人間の体が完全に伸びるにはかなりの時間がかかるうえ、競技規則において「GKはキッカーのシュートが放たれるまでゴールライン上を外れてはならない」というルールまであるため、「PKにおいてはキッカー側が圧倒的に有利である」という統計にも納得ができるかと思います。

従って、GKは「"ダイビング・エンベロープ"の内側であれば、無理なくPKをセーブすることができるが、この範囲の外側のボールを止めることは非常に困難となる」と言えます。この仮説に基づけば、ゴールキーパーが到達するのが最も難しいのはゴールの上隅(白の波線で囲ってある領域)であり、これは数学的にも簡単に証明を行うことができます。

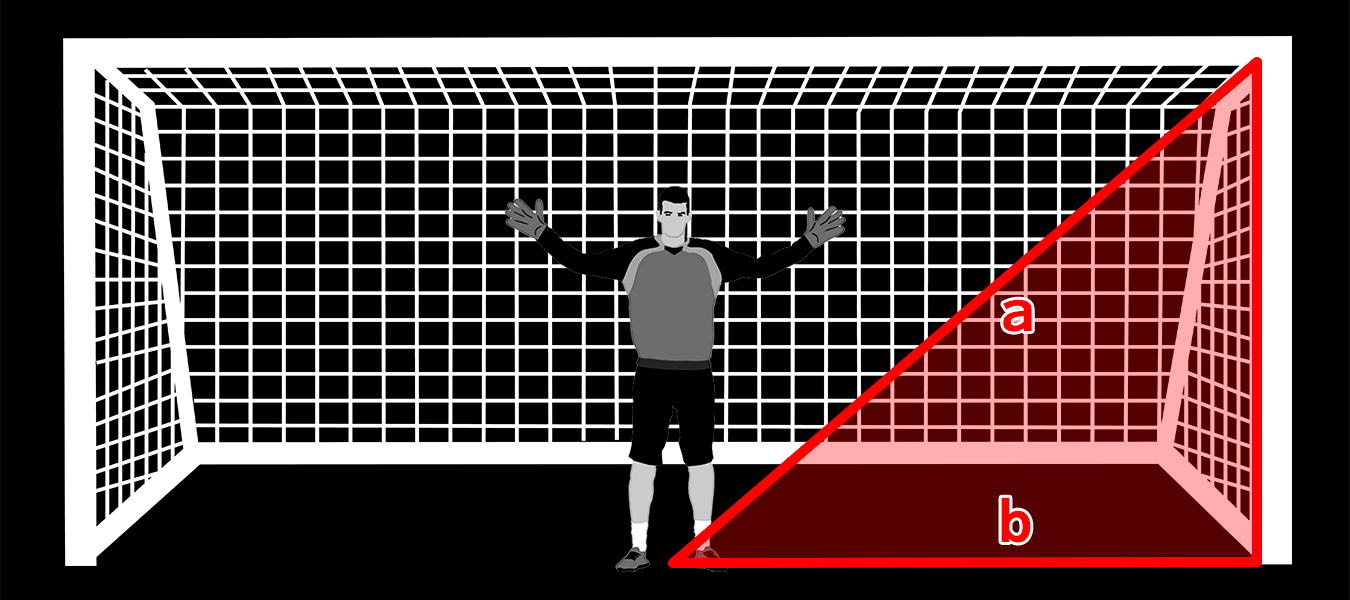図2: ゴールキーパーが”ゴール右上”に向かうボールを止めるために到達しなければならない距離(a)と”ゴール右下”に向かうボールを止めるために到達しなければならない距離(b)

ゴールキーパーの飛び込みを「直角三角形の2辺の長さ」に見立ててみると、なぜゴールの上隅が最も到達しにくい場所なのかが理解できるかと思います。ゴールキーパーが図2における三角形の左下の角(ゴールの中心付近)から動作をスタートする場合、上部の角(長さa)までの進路は斜辺の長さ、下部の角(長さb)までの進路は底辺の長さとなり、斜辺は直角三角形の中で最大の長さとなる訳なので、結果的に上隅への距離が最も長くなり、ゴールキーパーがセーブするのに「最も難しいゾーン」と定義できるのです。

計算を始める前に、予め必要な数値を整理しておきましょう。標準的なサッカーゴールは幅7.31m、高さ2.44メートルです。また、ペナルティースポット(ボールが置かれる場所)からゴールまでの距離は10.97mとなるので、対応する2つのベクトルを設定し、右上隅に向かうシュートの角度を求めるのに使用します。あと、少し細かいですが、ボールがゴールポストにぶつかっては意味がないので、ボールの半径をゴールの垂直方向と水平方向の寸法から引いておきましょう。規定のサッカーボールの半径は11cmなので…

11cm = 0.11m
x → 7.31 ÷ 2 = 3.655m (センターからポストまで) → 3.655-0.11 = 3.545m
y → 2.44-0.11 = 2.33m

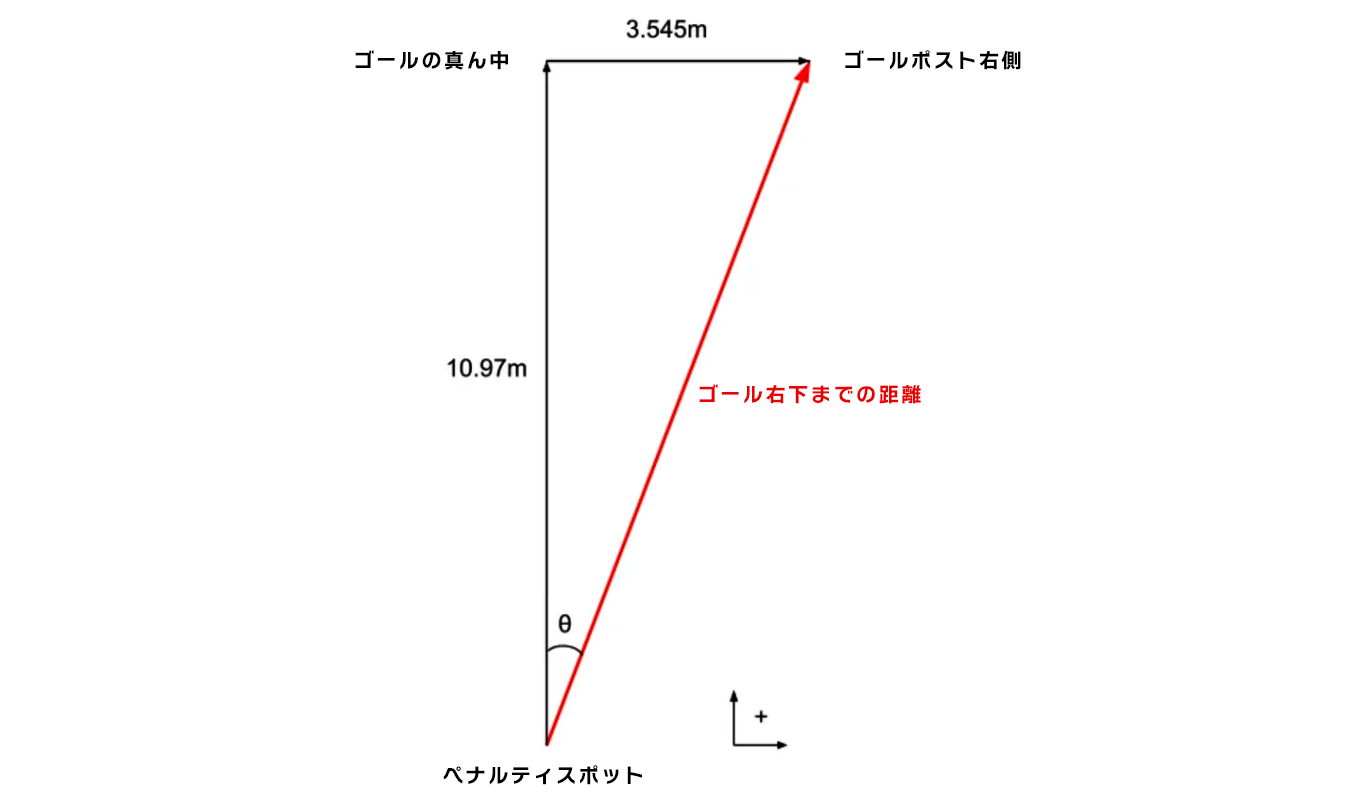図3: 水平方向にみた理想的なシュートの角度

図3のベクトルをもとに、角度θ(水平方向のシュートの角度)を求めます。ピタゴラスの定理を使って「底角までの距離」を求めると、垂直方向のシュートの角度を求める際に役立ちます。

θ = tan^-1 (底辺/高さ)
θ = tan^-1 (3.545/10.97)
θ = tan^-1 (0.323)
θ = 17.9°

d^2 = a^2 +b^2
d^2 = 10.97^2 + 3.545^2
d^2 = 120.34 + 12.57
d^2 = 132.91
d = √132.91
d = 11.53m

また、図4のベクトル図において、シュートの水平方向の要素を求めるために使用したのと同じ過程が、垂直方向のショット角度(θ)と「ゴール右上までの距離」(d=斜辺)を求めるためにそのまま適用できます。

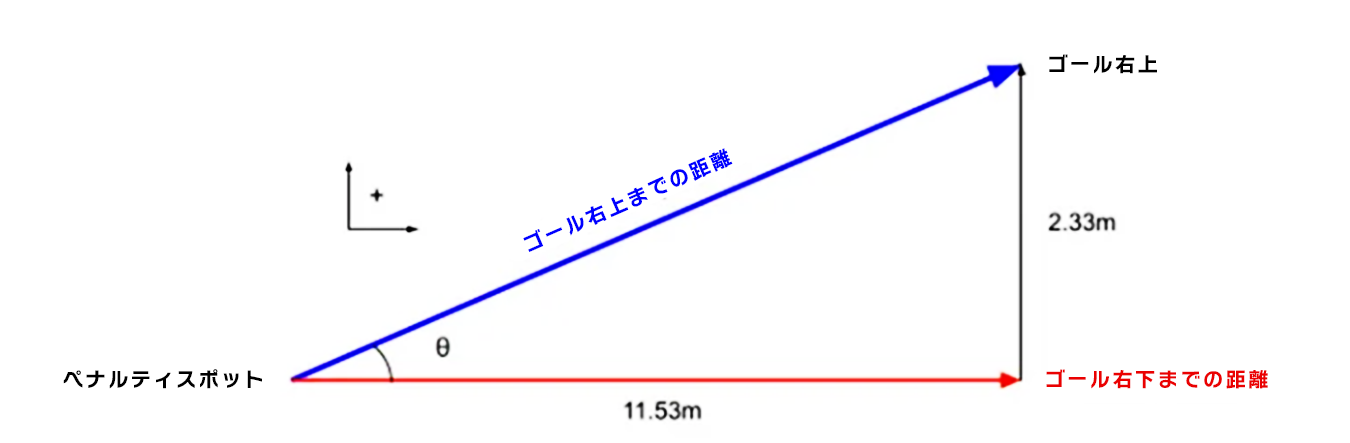図4: シュートの縦方向のベクトル図

θ = tan^-1 (底辺/高さ)
θ = tan^-1 (2.33/11.53)
θ = tan^-1 (0.2021)
θ = 11.42°

d^2 = a^2 +b^2
d^2 = 11.53^2 + 2.33^2
d^2 = 132.94 + 5.429
d^2 = 138.37
d = √138.37
d = 11.76m

これにより、水平角17.9° 前方へ垂直角11.4° で右上隅に向かってボールを蹴ることで、理論上は「ペナルティーキックを必ず成功させることが可能」と言えます。

なお上記の計算式では「ペナルティーキックがゴールとして記録されるまでに、ボールは11.76メートル移動する」と定義されました。ただ、ここで1つの疑問が浮かびあがります。もし相手GKがキックを完璧に読み、その正確な方向に飛び込もうとしていたらどうなるのでしょうか？本当に「必ず成功させることが可能」と言い切れるでしょうか？

その②: 速度

ゴールキーパーは、キッカーがPKを放つ前にゴールラインから前方に動くことはできませんが、ゴールライン上に沿って左右に動くことは可能となっています。つまりこの仮説では、GKが(キッカー側からみて)ゴールの右側に寄ることを選択することで、「もしかしたら…セーブされてしまう？」という可能性も出てきます。

ペナルティーキックを確実に決める上で2番目に重要な要素、それはボールの"速度"です。たとえGKが完璧にコースを読み、セービングの範囲内であったとしても、ボールの速度が速すぎることで、GKは反応できたとしてもセーブする時間はありません。当記事の冒頭に貼ったショート動画にもあるように、「コースが甘くても、フルパワーでシュートを打てばええんや！」という脳筋理論が成立してしまうのもそのためです。

2006年11月26日、当時ヘルタ・ベルリンに所属していた”ロニー”ことロニー・エベルソン・フルタード・デ・アラウージョが、公式に記録されたものの中でのサッカー史上最速(時速210.9km)とされるシュートを決めました。直接フリーキックからのゴールということで壁があったのも影響しているとは思いますが、ゴールキーパーいわく「ボールの位置に気づいたのは、ボールがゴールネットに吸い込まれた後だった」とのこと。

実際、視覚刺激(視覚を通じて環境や生理的な変化を検知すること)は、脳の運動野に到達するのに約9ミリ秒しかかからないと言われていますが、視覚刺激は目の網膜で光子を検出して脳に生体電気信号を送るプロセスが複雑なため、実際のところは平均30ミリ秒かかるそうです。何が言いたいのかというと、とにかく"至近距離から凄いスピードで飛んでくるボールに反応すること"に関しては、物理的にも生物学的にも"ほぼ無理ゲー"と言うことです。

◾︎ Ronny's Rocket - Fast Free Kick Goal!

では、時速210.9kmのボールが11.76m進むのにかかる時間を求めてみましょう。あらかじめ、速度をm/s(秒速メートル)に変換してから計算することにします。

速度の単位変換 → 210.9km/1h x 1000m/1km x 1h/3600s = 58.58m/s

v = d/t
t = d/v
t = 11.76/58.58
t = 0.2s

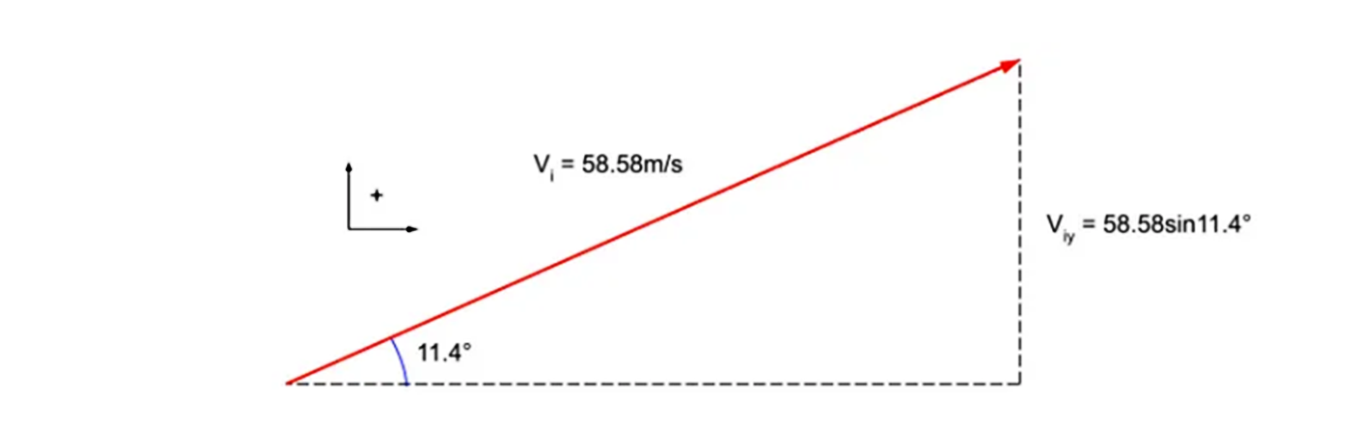図5: ボールの初速度

Viy = 58.58sin11.4° = 11.58m/s [Up]

d = Viy(t) + ½at^2
d = 11.58(0.2) + ½(-9.8)(0.2)^2
d = 2.316-0.196
d = 2.12m [Up]

なお、下向きの重力加速度を考慮すると、ゴールに入ったときのボールの実際の高さは地面から2.12メートルで、前に推測された高さ2.33メートルと比べると21cmのズレが生じます。しかし、ボールの垂直方向の到達地点が多少変わった程度では、図1で示した「セーブ不可ゾーン」内に収まるため、当記事において確立したシュートの角度と速度をもってすれば、GKにとって”セーブ不可能”なペナルティーキックとなるのです。

補足: そのボール、本当にセーブしても大丈夫？

一般論として「150J(ジュール)以上の運動エネルギーを持つ物体は、頭蓋骨への直撃で致命傷となる可能性がある」とされています。上記で仮定した速度のシュートにおけるサッカーボールが”危険な運動エネルギー”を持っていたとしたらあまりにも危なすぎるので、念の為そちらも計算しておきましょう。なお、ボールの質量は0.43kgとし、ボールの速度は前途した通り速度58.58m/sとします。

EK = 0.5mv^2
EK = 0.5(0.43)(58.58)^2
EK = 737.8J

危険とされる運動エネルギーの約5倍(!)に相当する数値が出てしまいました。かのアイザック・ニュートンが提唱した「運動量保存の法則」でも証明されているように、孤立した2つの物体が衝突した場合、衝突前後の運動量は保存されてしまうため、深刻な筋骨格系の外傷もしくは臓器へのダメージが懸念されます。

よって、737.8Jの運動エネルギーを持つボールが飛んできたことが判り次第、ゴールキーパーは即座にセービングを諦め、ボールを見送ることが望ましいでしょう。

まとめ

実際はどんなにテクニックがあり、かつ経験が豊富なトッププレーヤーであっても、この仮説で証明されているような”完璧なシュート”を決めるのはほぼ不可能です。人間はロボットではないし、微細な調整や状況判断は、理論だけでは太刀打ちできません。

勿論、このような座学も時には役に立つこともあるでしょうが、結局は日々のトレーニングと実践がモノを言います。何度もシュート練習を行うことで、きっと自分だけの「最強のペナルティーキック理論」を編み出すことができるでしょう。努力の積み重ねの先にこそ、ゴールネットを揺らす歓喜が待っているのです！